√99以上 比例 グラフ 式 940044-比例 表 式 グラフ
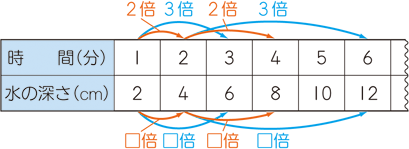
比例の式を定める x に値を代入する 問題3 (図を描けば何でもない話で,教科書にも出ていますが,言葉で言えばコテコテするので,難しいと思うかもしれない) (1) 比例のグラフ y=3x において, x の値が a (≠0) からその2倍の 2a に変化するとき, y比例とは? 簡単にいうと、比例とは・・・ 比例=比が等しい y=ax(aは0でない定数) グラフは原点を通る直線 ちょっとわかりやすく説明するわね。 比例というのは、片方が2倍・3倍となる時、もう片方も2倍・3倍と同じようになること。 つまり、 比比例の式とグラフ・比例定数・変域の解説 比例のグラフや表などは小学校のときに少しだけ習いましたが、中学校数学ではもう少し深く学びます。 主に「関数とはなにか」という最も簡単な例として最初に比例を教わります。 比例は「関数」の一種です

中学1年生の数学 グラフ グラフから式を求める 塾講師が数学をやりmath
比例 表 式 グラフ
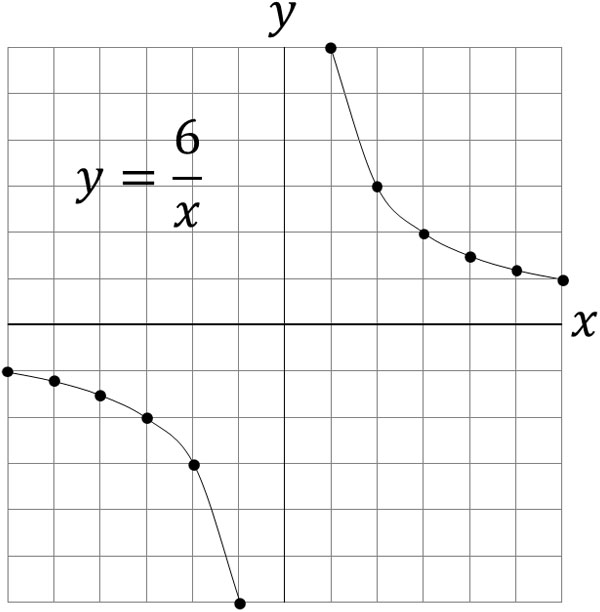
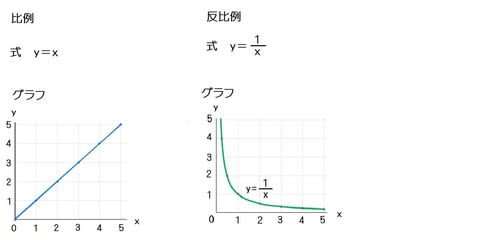
比例 表 式 グラフ- 比例のグラフの性質 比例の式 y = a x のグラフは、原点を通る直線となる。 比例定数 a が正なら、右肩上がりの直線となり、 a が負なら、右肩下がりの直線となる。 直線は、2つの点を決めれば1つに決まります。 原点を通ることがわかっているので、比例 それでは、実際にグラフを書いてみましょう。 グラフが通る点を取っていくために、まずは反比例の式に を代入します。 を に代入すると このことから、反比例のグラフは のとき を通るということが分かります。 かず先生 これで点が1つ取れたね



比例とは 比例定数の求め方やグラフの書き方 計算問題 受験辞典
ここまで解いてみてわかったと思いますが、1次関数のグラフの応用問題は、まずグラフに書くのがポイントです。 グラフを書いたあとで、 「何に注目したのか」「何に気が付いたのか」「どんな予測が立ったのか」「何を試したのか」 などの経験値を積む を の式で表す時には必ず求めなければならないものですので確認しておきます。 比例定数の求め方は、シンプルです。 比例定数を とおくと、 = で求めることができます。 これは、先ほど登場した の両辺を で割ったものです。 試しに例題をあげておきます。 例題 は に比例し、 のとき、 です。 この時の比例定数を求めよ。 例題の解答・解説 = を使えば一瞬です。 比例定数 は = = とこのとき比例定数a=2となる。 つまりy=2x ② グラフ上にx=1の点をとる。 ≫ 座標は (1,3)である。 これは原点からx方向に+1進んだら y方向に3進むことになる。 ≫ このとき比例定数a= 3となる。 つまりy=3x 練習 ①,②のグラフの式を求めよ。 x y O ① ② 答表示 関数 要点 関数 比例 反比例 座標 比例のグラフ 反比例のグラフ 関数 例題 変域 比例 比例の式の出し方 反比例 反比例の式 座標 比例の
比例のグラフ手順 原点に点をとる 比例定数を見て、分母の数だけ右へ分子の数だけ上下に動かしたところに点をとる 2点を線で結ぶ 以上! この3ステップでグラフが書けてしまいます。 それでは この式をグラフにしてみます。 手順通り1つずつ確認し 比例のグラフ 座標平面上での点について見てきましたが、今度は比例のグラフについて考えてみます。 y = 2x y = 2 x について考えてみましょう。 値の対応表をかくと、次のようになります。 これらに対応する点をとっていってみましょう。 つまり、 x = 1 エクセルでの比例のグラフ作成のやり方を教えていただけないでしょうか グラフに使うプロットを別々のセルに入力します。 Excelで比例式の計算が出来る関数はありますか? また、あるのなら何という関数を使えばいいのですか?
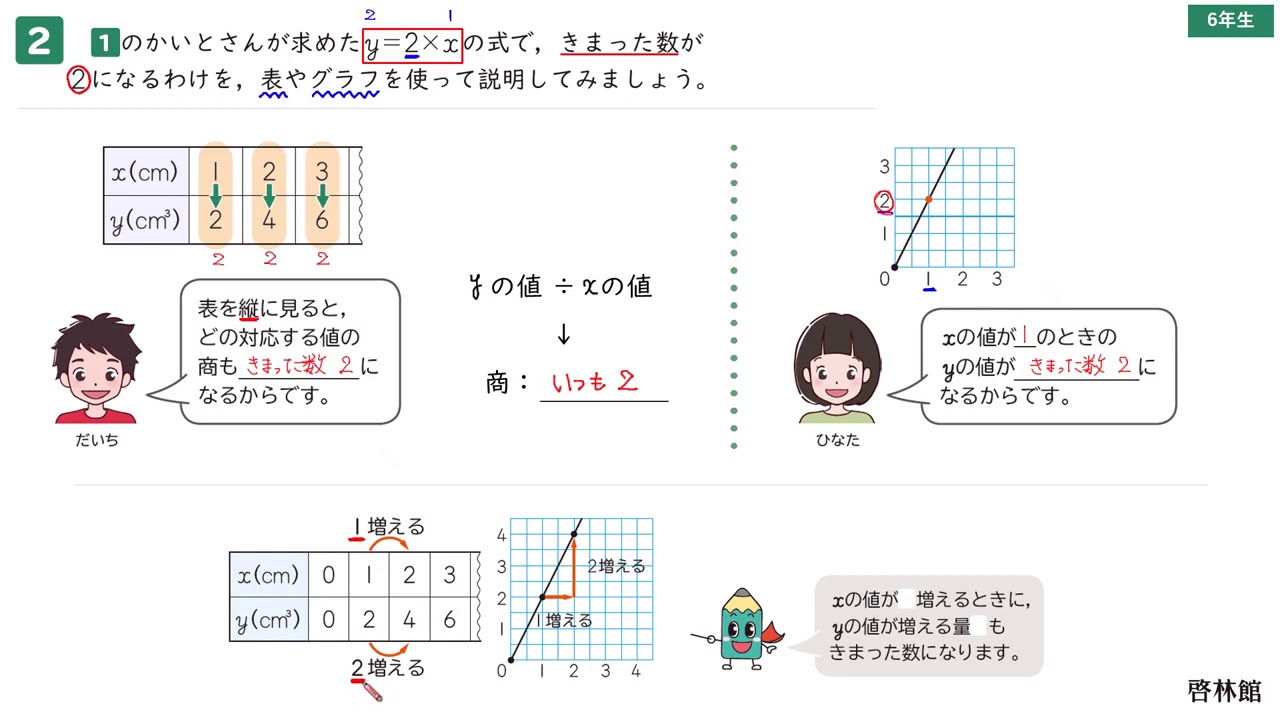
上で挙げた比例の性質を満たしているのが分かりますね。 針金の長さを x(m) x ( m ) 、重さを y(g) y ( g ) とすると、これらの関係は「 y=5× x y = 5 × x 」 と表すことができます。 このように、 y= y = 決まった数×x × x という形が比例の式です。 この式の形を抑えておきましょう。 そしてもう一つ抑えておくべきなのが、比例のグラフです。 針金の長さと重さの関係をグラフに表すと ・比例の式の求め方 = y = a × x a は「比例定数」 a = y x = y ÷ x で 求めることができる ・比例の式の問題の解き方 「 y は x に比例し〜」→ = y = a x を用意 x と y を「代入」して a を求める ・座標 A ( , ) ( a , b ) の a を x 座標 b を y 座標 ・比例のグラフの書き方 x と y の表を作る 整数の x と y を見つける グラフに、その点をとる その点と原点を通る「直線」を引く ・比例比例の関係を数式にすると、y=kxとなります(kは定数)。 この比例の関係をエクセル上で関数として入力し、計算していきます。 まずは、以下のようにxの値を1刻みで入力してみましょう。 今回はk=2という比例定数の比例の式を求めていきます。 続い




比例のグラフ 無料で使える中学学習プリント
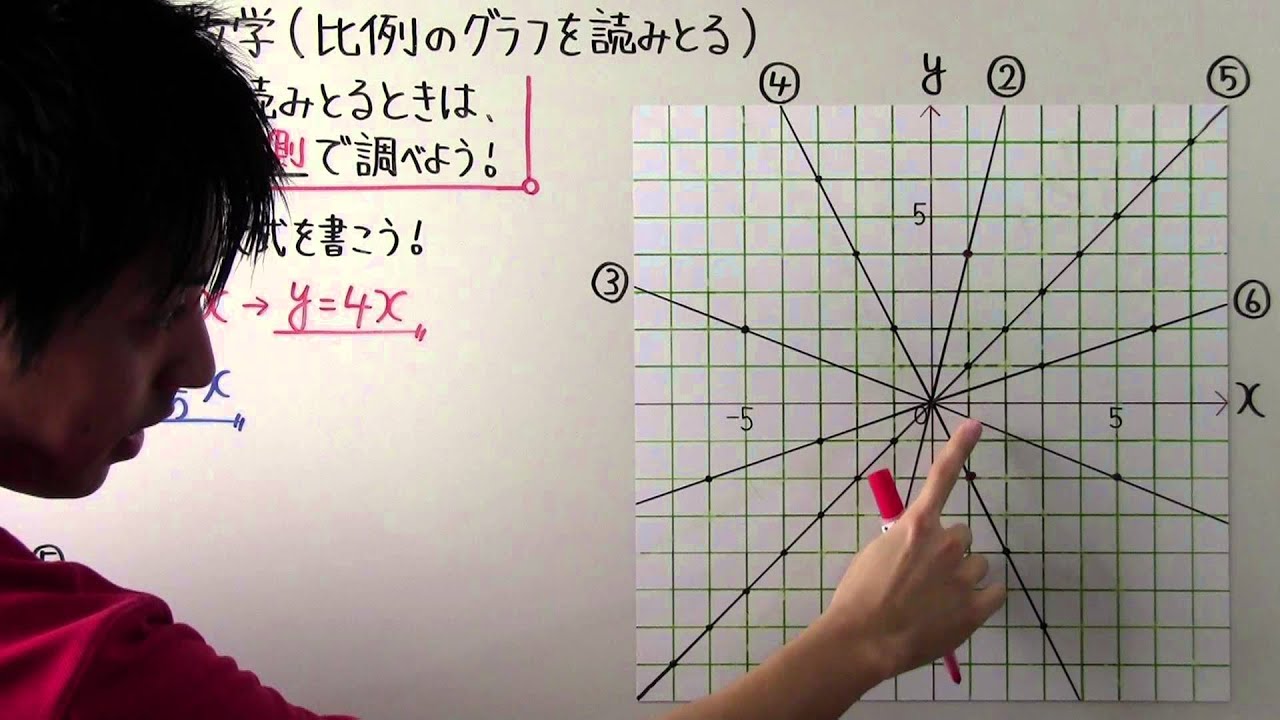



中1 数学 中1 50 比例のグラフを読みとる Youtube
関数のグラフは、ある式を満たす 点の集合 です。 比例の関係であれば、比例の式を満たすxとyの値を、x座標とy座標として、座標上に点をとっていくことで、グラフを書くことができます。 つまり、 直線の通る2点が分かれば、グラフが書ける ということ こんにちは、ウチダです。 今日は、小学6年生および中学1年生で習う 「比例・反比例」 の式のグラフの書き方や比例定数の求め方、またそれらの意味や代表例についてわかりやすく解説していきます。 ※この記事では比例と反比例をセットで解説していきままず「比例」とは、 y=ax(aは比例定数) で表される関係のことだったよね。 「グラフ」とは、式で書かれたものを、目に見える形に表すことだよ。 比例の式 y=ax(aは比例定数) の式を、グラフで表すときのポイントは、次の通りだよ。 POINT 実際にy
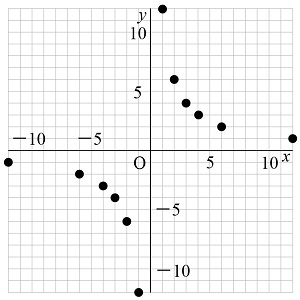



中1数学 反比例の式 グラフってどういうもの まなビタミン By 東京個別指導学院
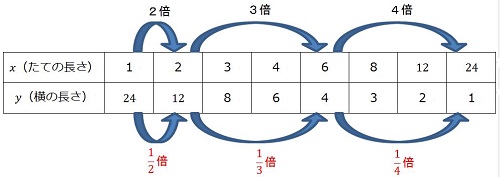



中1数学 反比例の式 グラフってどういうもの まなビタミン By 東京個別指導学院
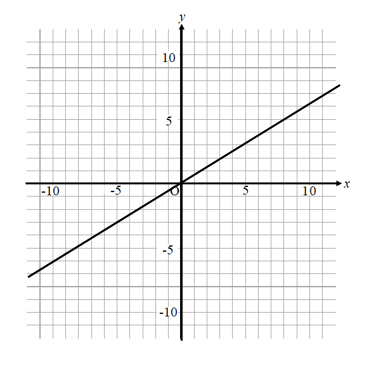
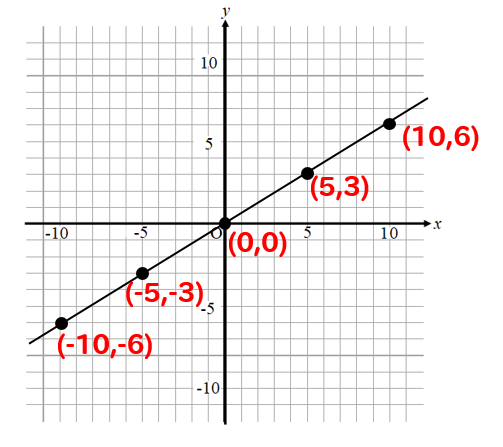
それでは手順通り、こちらのグラフを式にしてみます。 まずは手順① グラフの通る座標を読み取りましょう。 グラフの直線上を見ていって 目盛り上にぴったり重なっているところに点をとっていくと このように座標を読み取ることができます。 これらの中から原点 (0,0)以外の点を選びます。 (なるべく数が小さいのを選びましょう) 今回は (5,3)という座標を選びます。 これは 『 x =5のと ここでは、比例のグラフをきれいに、簡単に書く方法を紹介していきます。 例題 のグラフを書け。 STEP1 軸を用意する まずは、グラフを書くための準備をしましょう。 軸、 軸を書き、原点 を記入します。 STEP2 原点に点を打つ 先ほど述べたように、比例のグラフは必ず 原点を通る直線 になります。 原点 に点を打ちましょう。 STEP3 もう 1 か所に点を打つ 原点の座標はわかってい 「yはxに反比例し」ですから、「 y= 」の式を使います。 解き方は以下の通りです。 (1):x=2,y=6を y= に代入しaの値を求め、その値を y= に代入する。 (2): (1)で求めた式に、x=4を代入する。 「代入する」というのが何回か出てきていますね。 そう、この「代入する」というのが基本なのです。 答え (1) x=2,y=6を代入すると、 6= 両辺を2倍して、a=6 × 2=12 したがって、求
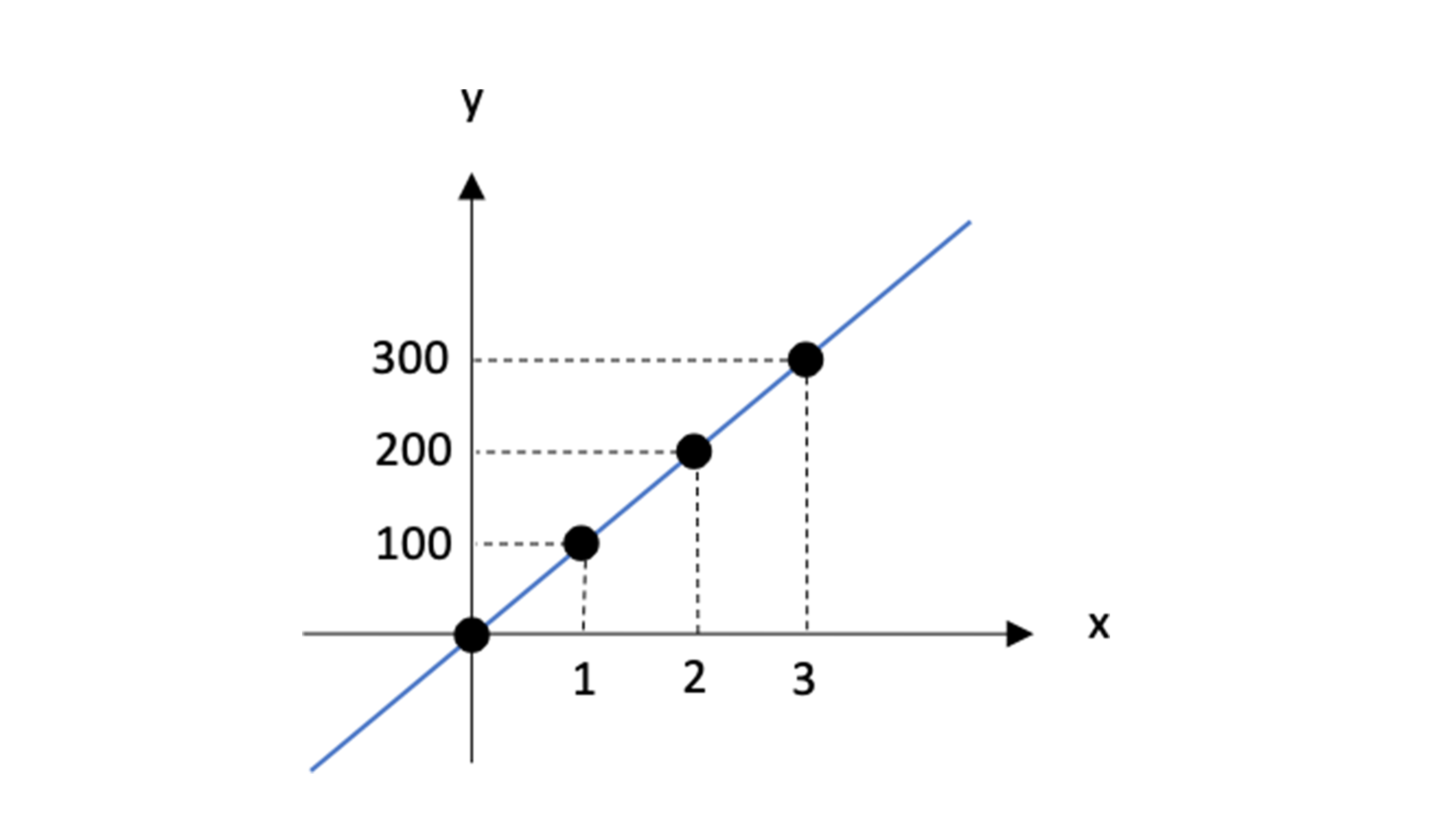



グラフが2本になるのに注意 比例 反比例 をおさらいしよう 受験に関する豆知識 学習塾ランキング検索総合サイト 塾プラス




比例のグラフから式を求める チーム エン
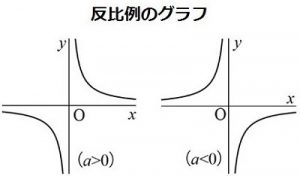
例題1下の比例のグラフについて次の問いに答えなさい。①このグラフの式を求めなさい②\(x\) の値が \(3\) のときの \(y\) の値を求めなさい。解答①グラフの式グラフのかき方を学習した今、この問題は難しくありませんね。比例y=axのグラフは直線になる。 グラフは必ず原点 (0,0)を通る。 比例定数aが正の数なら 右上がり のグラフに、 aが負の数なら 右下がり のグラフになる。 O x y y= 2 3 xのグラフ 比例定数が正だと グラフが 右上がり になる。 O x y y=2xのグラフ 比例定数aが負だと グラフが 右下がり になる。 比例のグラフ 例題と練習問題 例題 グラフから比例の式を求める問題1 グラフから比例の式を求める (反比例のグラフと面積の求め方 反比例のグラフと面積が関係する問題の解き方も比例のときと同じです。 グラフ、 座標上に各点を書き込む 、それだけで求めるものは三角形の面積か、四角形の面積です。 反比例の場合、1つ特別な性質を持っています。




中学1年生の数学 グラフ グラフから式を求める 塾講師が数学をやりmath



比例とは 比例定数の求め方やグラフの書き方 計算問題 受験辞典
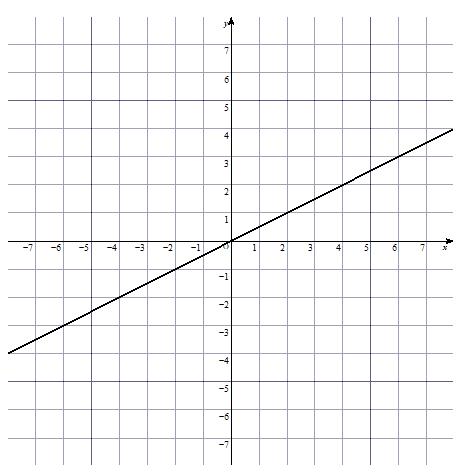
比例のグラフでは、必ず直線になります。 また、直線は必ず原点を通ります。 y = a x の公式から、グラフを作ることができます。 なお反対に、グラフから y = a x の式を出すこともできます。 例えば、 x が1つ増えるごとに y が2つ増えている場合、 y = 2 x の式だと分かります。 比例定数 a が正の数か負の数でグラフの形が異なる 比例の式を考えるとき、重要なことが他にあります。 それは、比例定 比例と反比例 1式とグラフ 今回は、中学1年生の 比例・反比例の基本 について解説します。 比例と反比例は、今後学習する1次関数や2次関数の基本となるので、しっかりとマスターしましょう。 特に分数のときに間違えやすいので気をつけましょう。 比例のグラフ では、比例のグラフを書いていきましょう。 最初は a = 2 の y = 2 x のグラフを見ていきましょう。 表の x と y の座標位置に点を打って繋げるとグラフになります。 比例のグラフは図のように 原点を通る直線 になります。 そして、 a > 0 ( a が正の数)だとグラフは右上がりに。 a < 0 ( a が負の数)だとグラフは右下がりになります。 こちらのグラフは y = − 1 2 x のグ



比例と反比例 1 式とグラフ ファクトリウム




グラフが2本になるのに注意 比例 反比例 をおさらいしよう 受験に関する豆知識 学習塾ランキング検索総合サイト 塾プラス
次の式に対応するグラフを,右から選びなさい. (ルール:式を一つクリックし,続けて「 対応するグラフ 」をクリックすると消えます.全部消えたらできあがりです.)また、グラフの点から比例の式を表すこともできます。ここまでの内容で、比例は最低限理解できたといえるでしょう! 今回の内容の練習問題があるので、よかったら理解度を確認してみてください! やってみよう 1次のグラフから式を導出してみよう。解説 さて、この式のグラフはどのようになるのか。 まず、比例の式は必ず原点 (0,0) ( 0, 0) を通ります。 次に、どのような座標を通るのか考えます。 x x 座標、 y y 座標ともに整数になる格子点でないと作図できませんので・・・ x= 3 x = 3 のとき、 y= 2 y



中1数学 反比例の式 グラフってどういうもの まなビタミン By 東京個別指導学院



比例 反比例の式 式の作り方 違いは 問題を使って解説するぞ 数スタ




比例の式とグラフ 比例定数 変域の解説 数学fun




中学数学1年 比例と反比例 Wikibooks



比例と反比例 中学数学の座標の読み方とグラフの式の求め方 Hatsudy 総合学習サイト
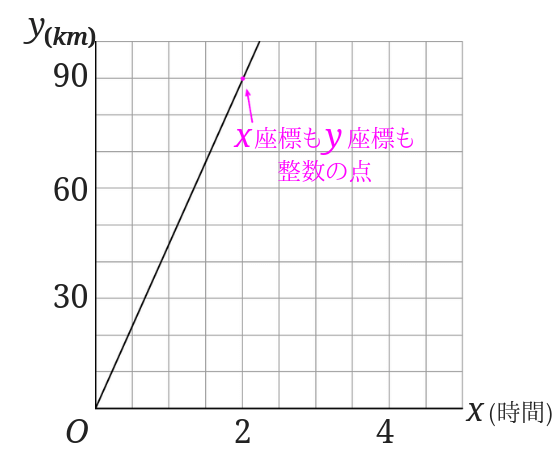



小学生の比例でグラフから式を求める時ってどうするの みけねこ小学校




比例のグラフ その2



比例のグラフから式を求める方法とは ラクな裏技の考え方とは 数スタ
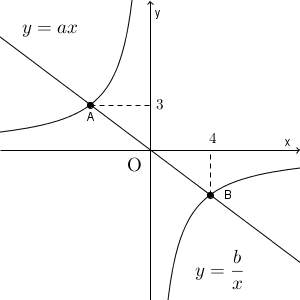



応用 比例と反比例のグラフ なかけんの数学ノート




書き方 反比例の双曲線グラフを5秒でかきおえる方法 Qikeru 学びを楽しくわかりやすく



無料 中1数学 テスト対策問題 解答プリント 121 比例と反比例2 比例2グラフ



Mathematics 比例と反比例 式と座標 働きアリ
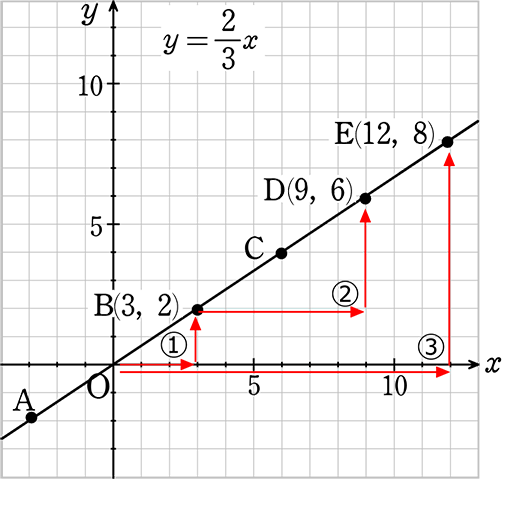



中学数学 比例 反比例




比例のグラフ 式を作る ມ ມມອງການຊ ວຍເຂ າເຖ ງ
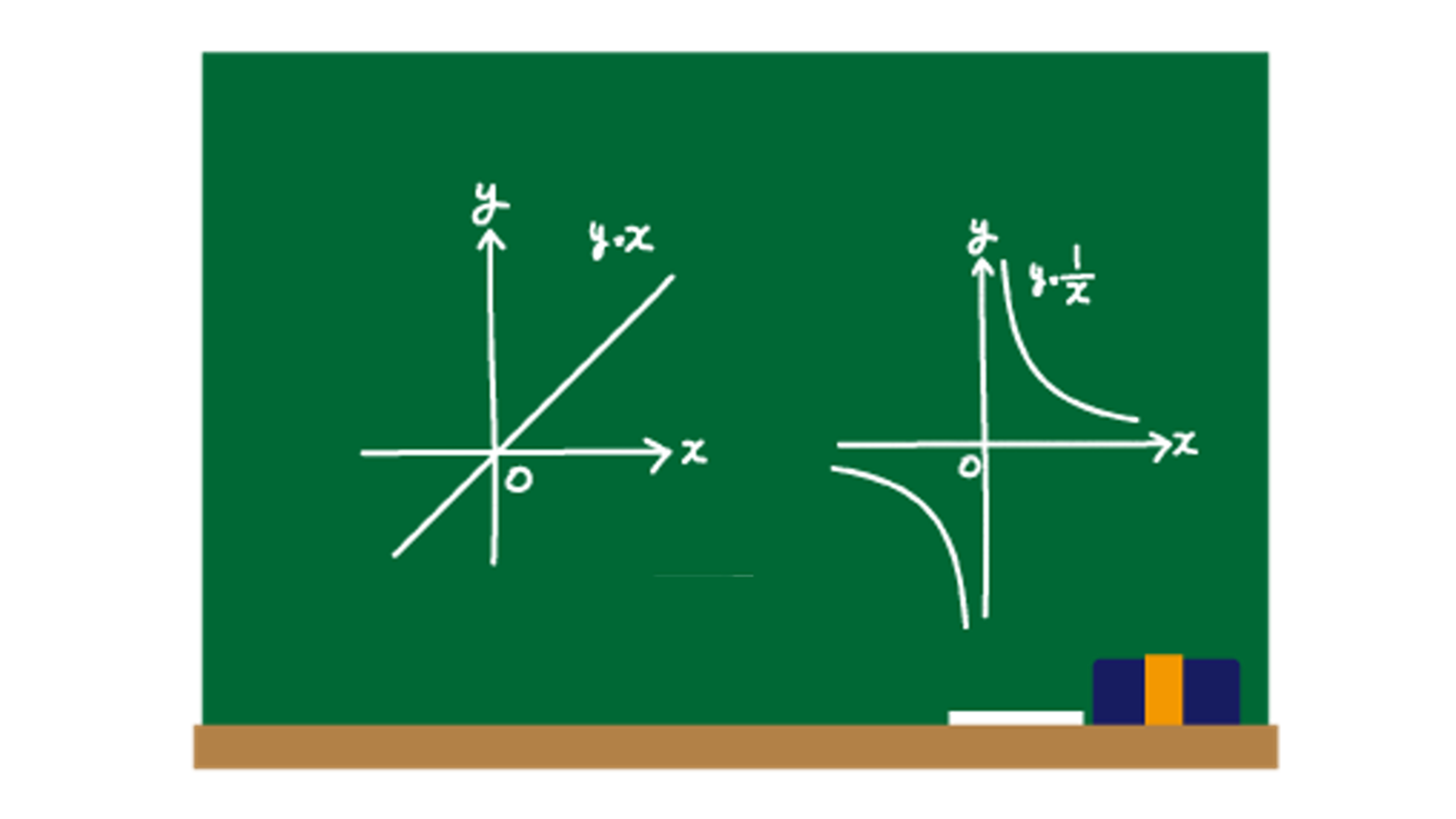



グラフが2本になるのに注意 比例 反比例 をおさらいしよう 受験に関する豆知識 学習塾ランキング検索総合サイト 塾プラス



Studydoctor反比例のグラフと式の求め方 中学1年数学 Studydoctor
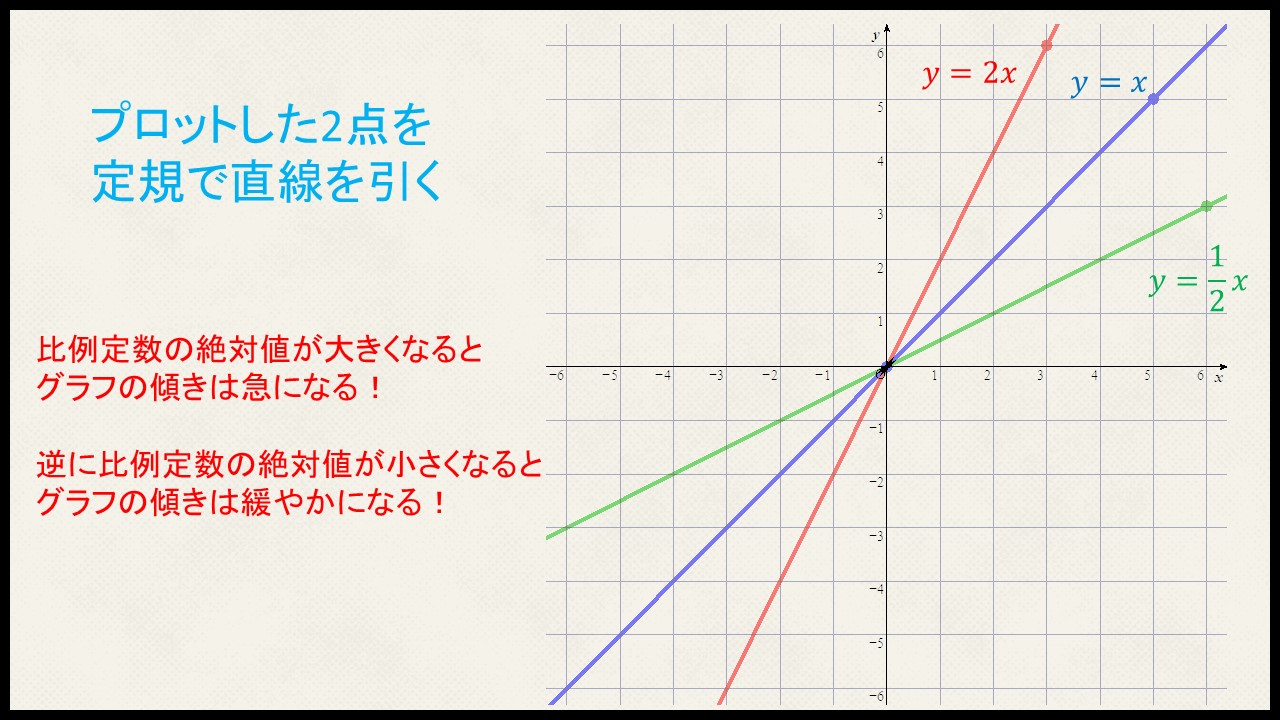



比例のグラフ その2
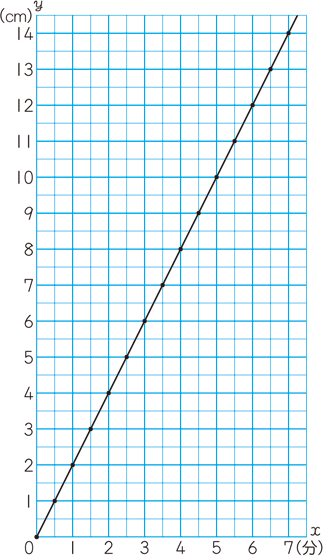



比例のグラフ 算数用語集




比例のグラフから式を求める方法とは ラクな裏技の考え方とは 数スタ




一次関数とは 式とグラフの解説 数学fun




中学数学1年 比例と反比例 Wikibooks
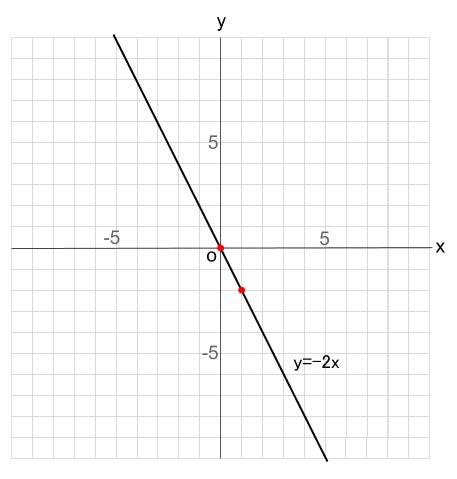



中学数学 比例のグラフをかく 中学数学の無料オンライン学習サイトchu Su
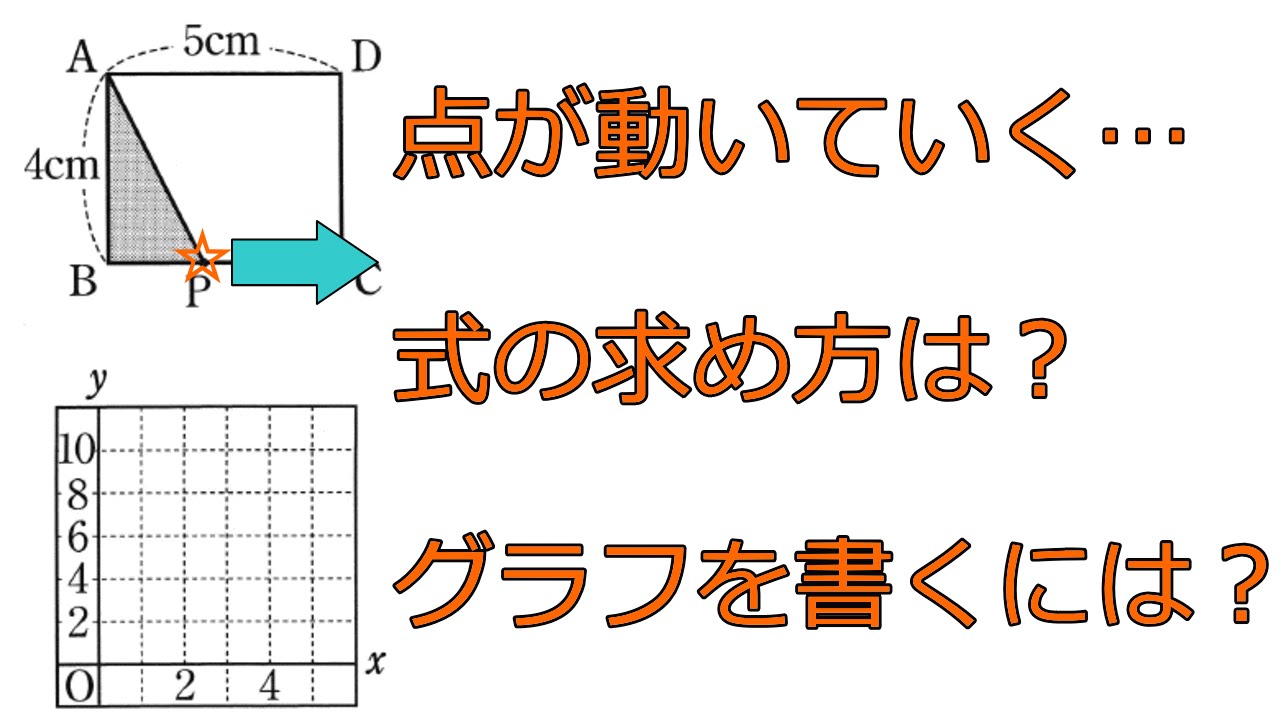



比例のグラフの利用 動点の問題の解き方 中学1年数学 Youtube



中1数学 反比例の式 グラフってどういうもの まなビタミン By 東京個別指導学院




中学数学 比例 反比例
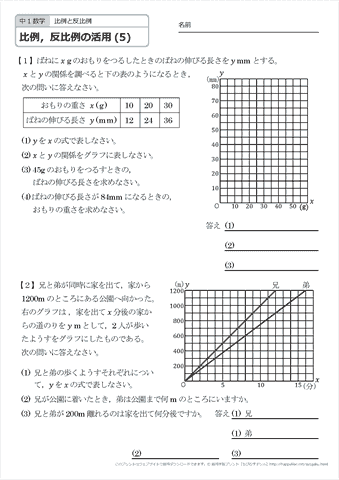



中学1年生 数学 比例 反比例の活用 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



1




比例の式と反比例の式 Geogebra




中学数学 比例のグラフ4つの特徴 Qikeru 学びを楽しくわかりやすく




小学6年生の算数 比例 練習問題プリント ちびむすドリル 小学生
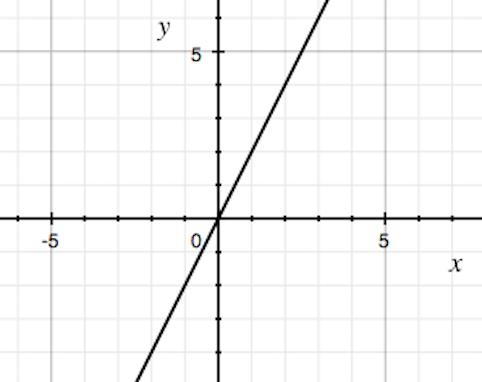



比例 練習問題 グラフから式を答える問題 苦手な数学を簡単に



比例とは 比例定数の求め方やグラフの書き方 計算問題 受験辞典
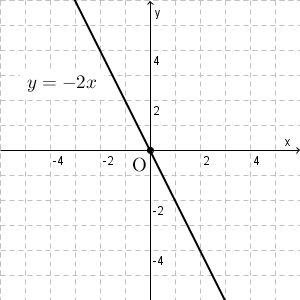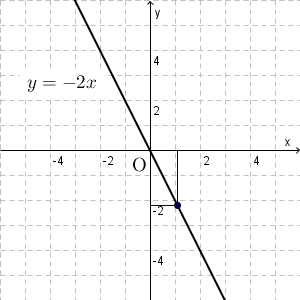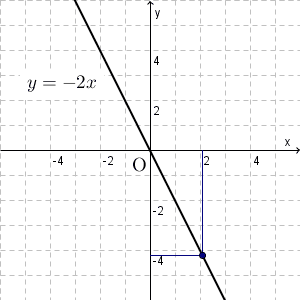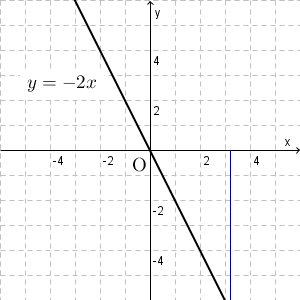



基本 比例のグラフの性質 なかけんの数学ノート




反比例の式とグラフ 数学fun



比例とは 比例定数の求め方やグラフの書き方 計算問題 受験辞典
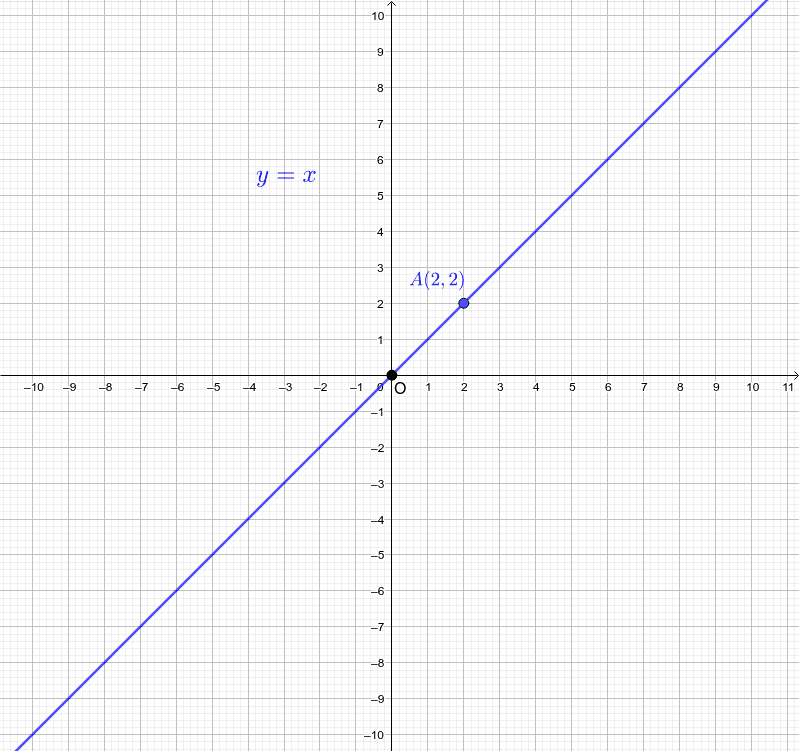



比例定数が分数のときの比例のグラフ Geogebra
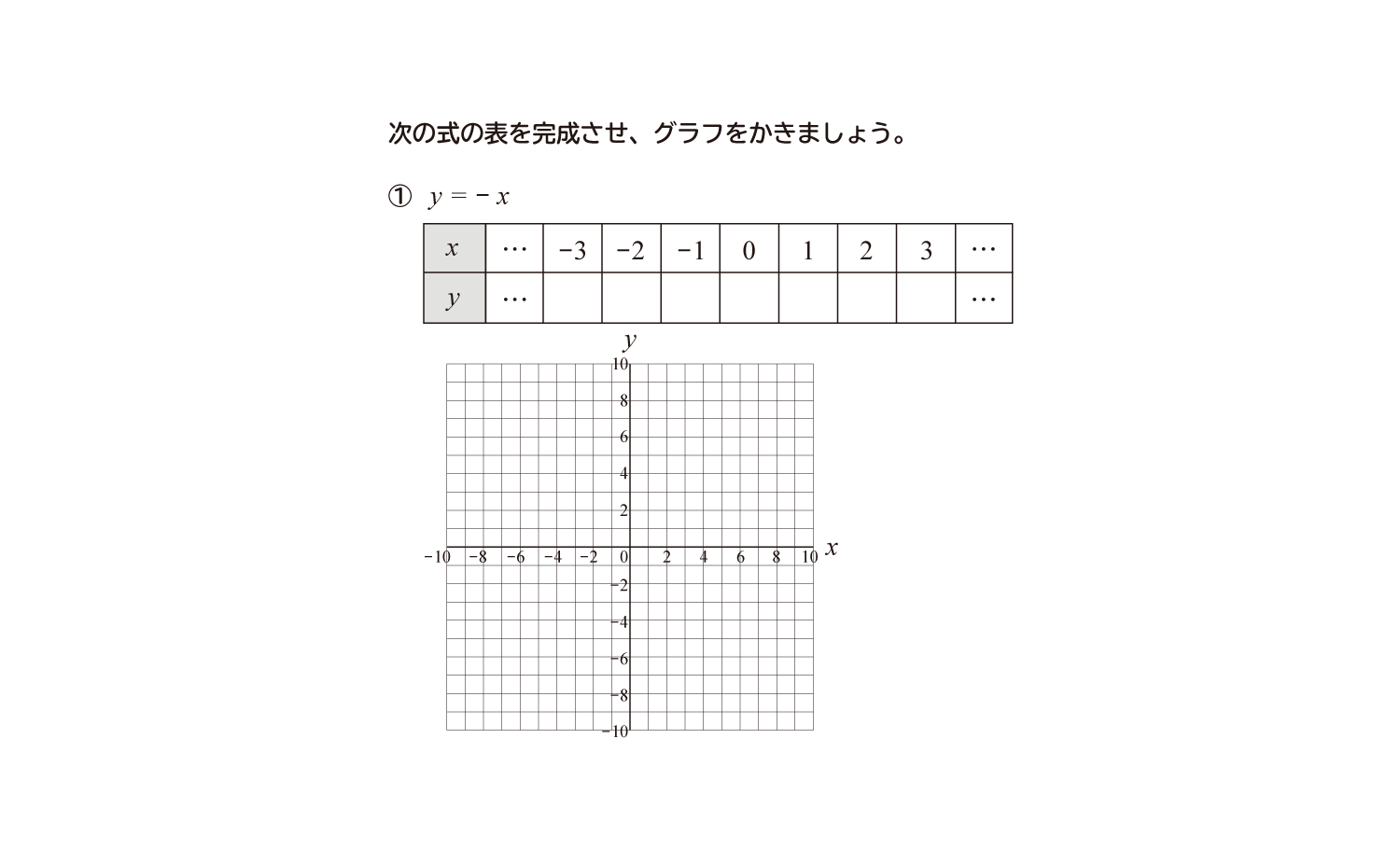



中学1年生 数学 無料問題集 比例のグラフ 比例定数が負の場合 おかわりドリル



2次関数 関数について 日々是鍛錬 ひびこれたんれん
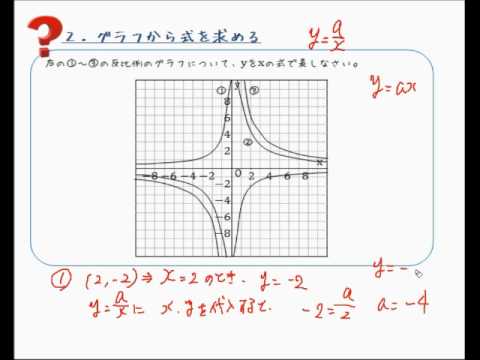



グラフから式を求める 反比例 Youtube



無料 中1数学 発展問題 問題プリント 比例と反比例6 利用1



二乗に比例とは 1分でわかる意味 式 グラフ 例 比例との違い



比例と反比例 比例 02 表 式 グラフを使って Youtube
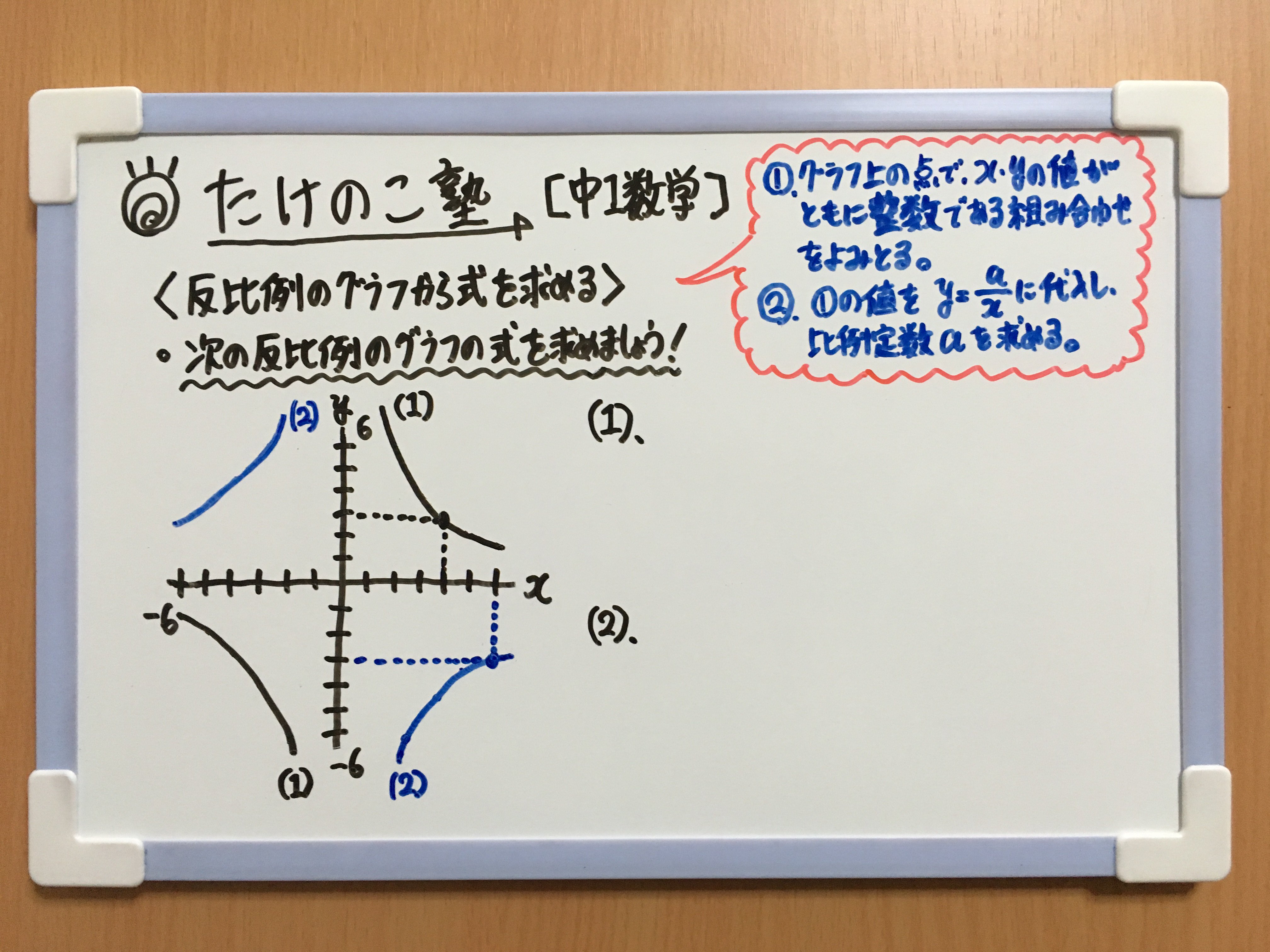



O Xrhsths たけのこ塾 Sto Twitter 中1数学 今回は 反比例のグラフから式を求める 問題です グラフから式を求める手順は次の通りです グラフ上の点で X Yの値がともに整数の組み合わせのものをよみとる そのx Yの値を 反比例の式 Y A X に代入し
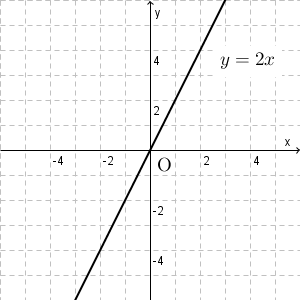



基本 比例のグラフの性質 なかけんの数学ノート




比例と反比例はこれで完璧 グラフと式の読み解き方



Studydoctor反比例のグラフと式の求め方 中学1年数学 Studydoctor
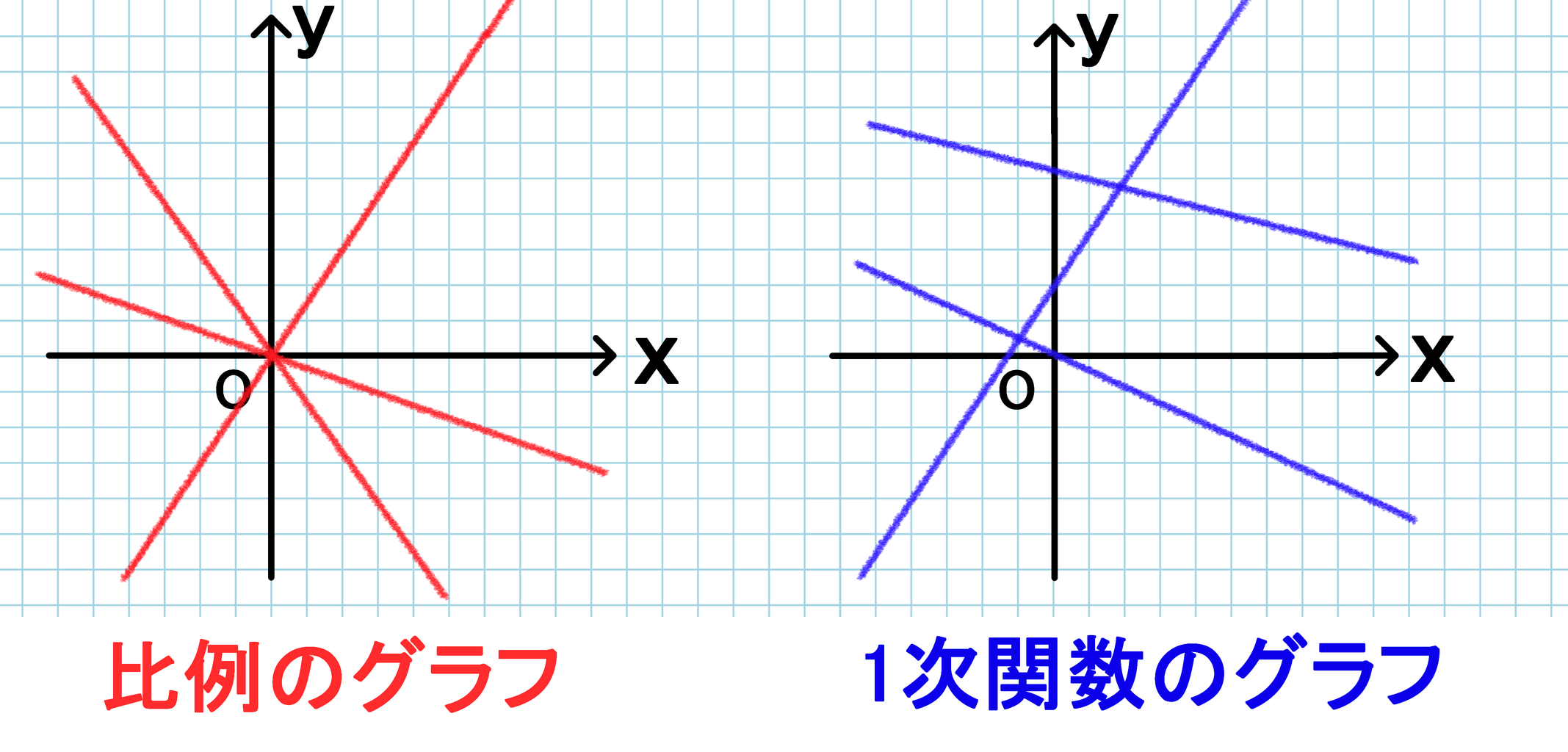



1次関数と比例の違いとは バカでもわかる 中学数学
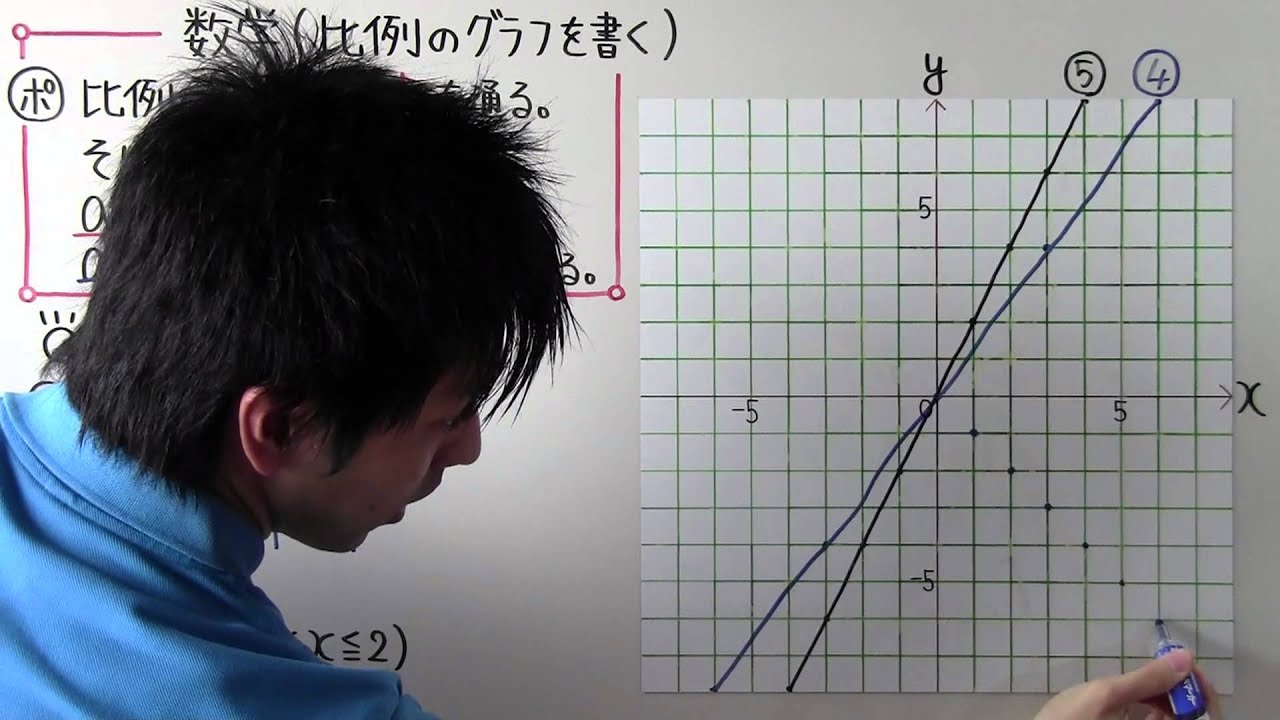



中1 数学 中1 49 比例のグラフを書く Youtube



Studydoctor比例のグラフの書き方と特徴 中学1年数学 Studydoctor



無料 中1数学 基本問題 解答プリント 比例と反比例5 反比例のグラフ 132



無料 中1数学 基本問題 解答プリント 比例と反比例4 反比例の式 131
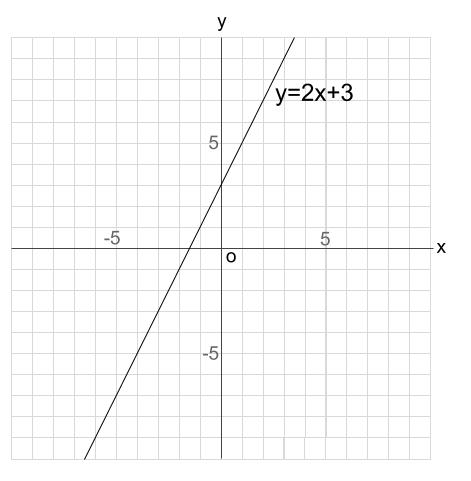



中学数学 1次関数のグラフ 中学数学の無料オンライン学習サイトchu Su




中学数学 比例のグラフ4つの特徴 Qikeru 学びを楽しくわかりやすく




中1数学 比例とは 比例の式と比例定数 グラフを解説 簡単 トムラボ




比例の表やグラフの性質 問題の解き方 小学生に教えるための解説 数学fun



Studydoctor比例 反比例のグラフと図形 中学1年数学 Studydoctor




比例の式とグラフ 比例定数 変域の解説 数学fun



1
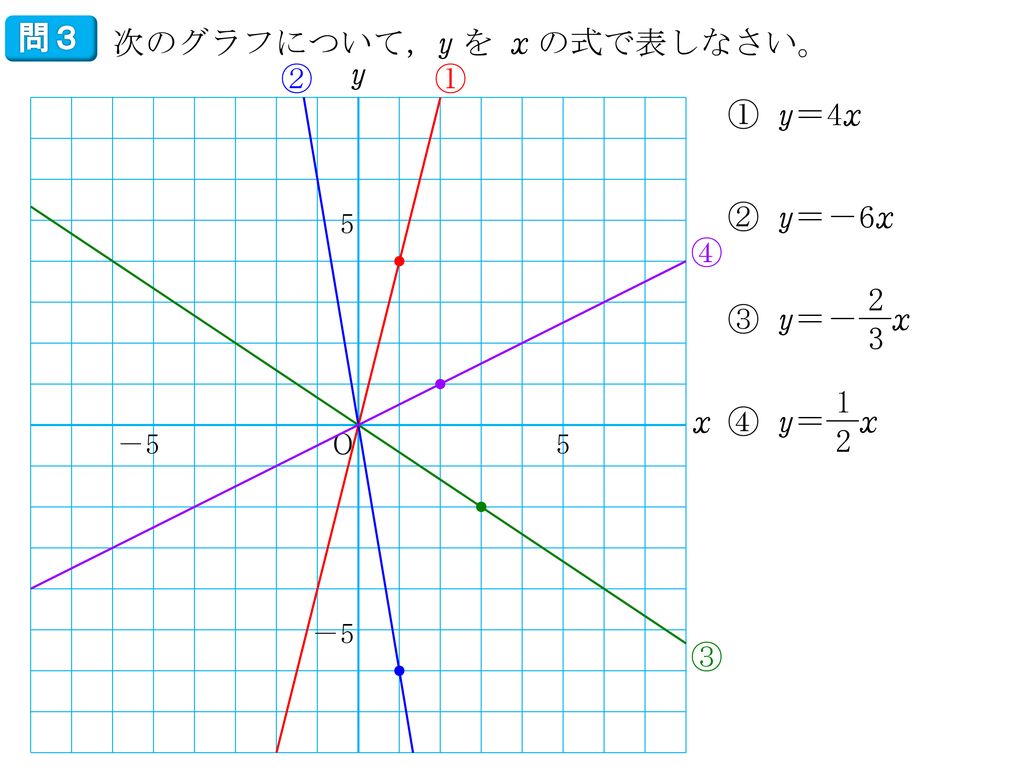



中学数学1年 4章 比例と反比例 2 比例 6時間 Ppt Download



反比例とは 式やグラフの書き方 記号 問題の解き方 受験辞典



比例と反比例 2 式を求める ファクトリウム



比例関係とは 1分でわかる意味 グラフ 正比例との違い 負比例
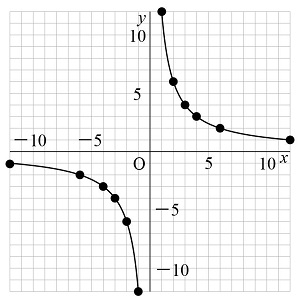



中1数学 反比例の式 グラフってどういうもの まなビタミン By 東京個別指導学院
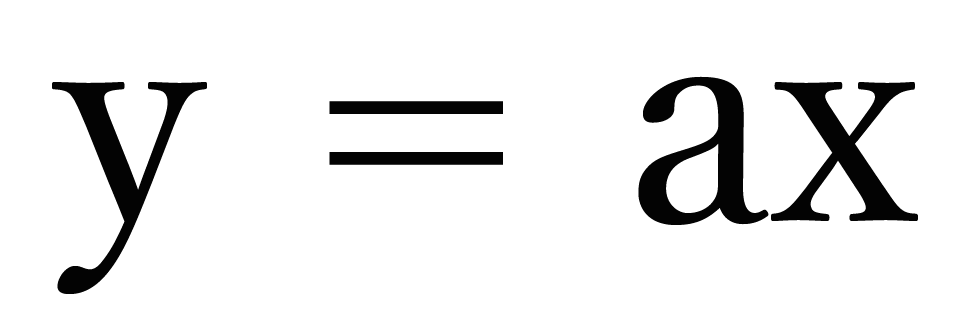



中学数学 比例のグラフ4つの特徴 Qikeru 学びを楽しくわかりやすく



比例と反比例 1 式とグラフ ファクトリウム



3




比例のグラフの特徴 Youtube



いざ いざ 実践 比例と反比例 小学6年 算数の教え方教えますmother S Math Happy Study Support



比例 算数用語集




反比例のグラフから式を求める チーム エン



比例のグラフから式を求める方法とは ラクな裏技の考え方とは 数スタ




2乗に比例する関数のグラフ 放物線 の書き方 無料で使える中学学習プリント
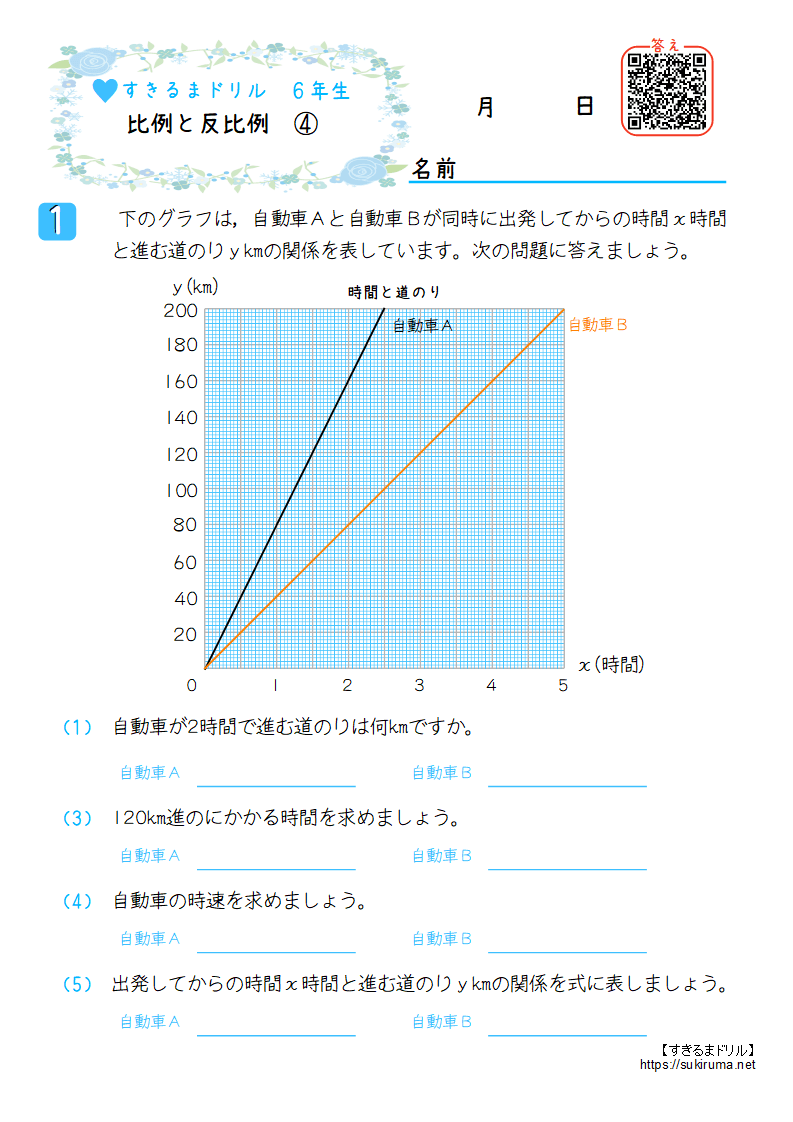



すきるまドリル 小学6年生 算数 比例と反比例 無料学習プリント すきるまドリル 幼児 小学生の無料学習プリント



小6 算数 小6 30 比例のグラフ Youtube




書き方 比例のグラフを3秒で書き上げる方法 Qikeru 学びを楽しくわかりやすく



Studydoctor比例のグラフの基本 中学1年数学 Studydoctor
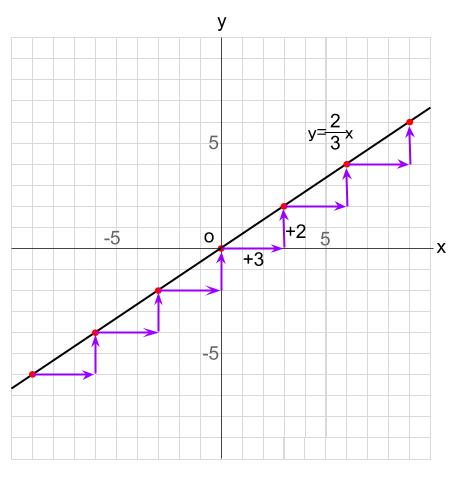



中学数学 比例のグラフをかく 中学数学の無料オンライン学習サイトchu Su




反比例の式とグラフ 数学fun




比例と反比例はこれで完璧 グラフと式の読み解き方




比例 反比例 一次関数 二次関数 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信



反比例とは 式やグラフの書き方 記号 問題の解き方 受験辞典
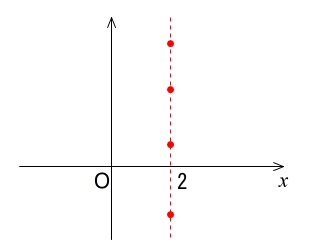



座標とは 比例と反比例の関数のグラフと座標の求め方
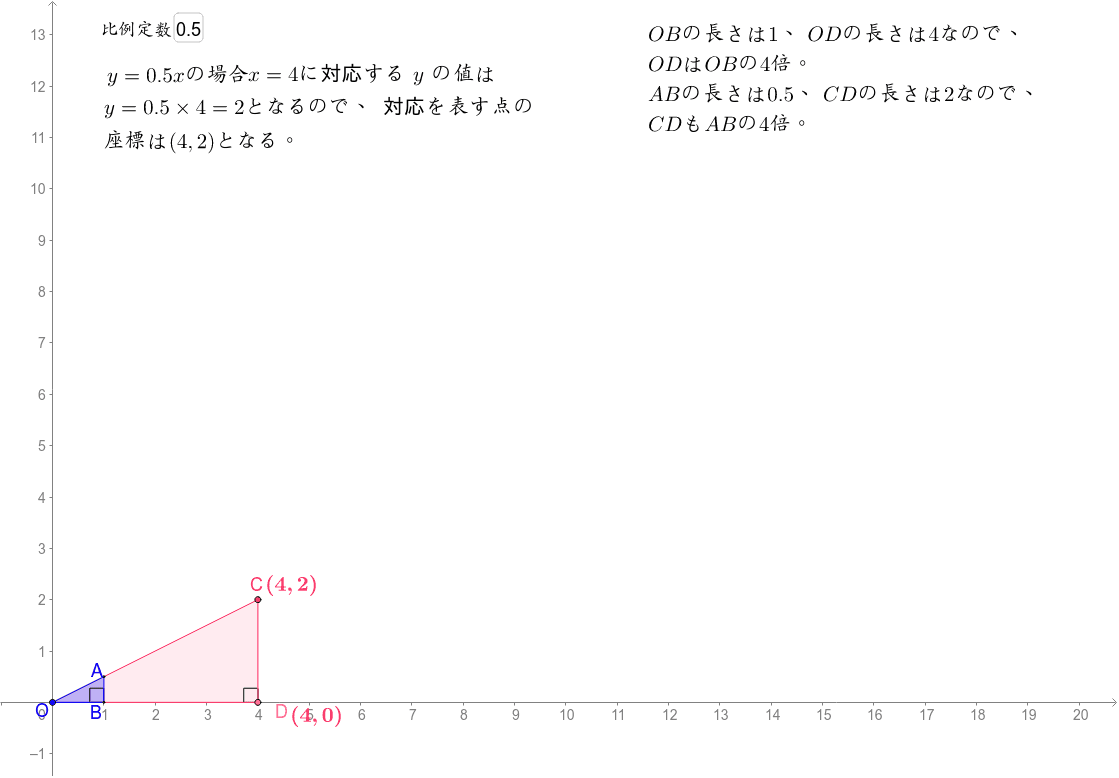



比例の式とグラフの形 Geogebra



中1 比例のグラフ



1
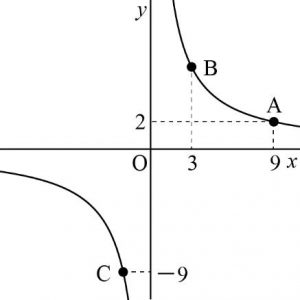



中1数学 反比例の式 グラフってどういうもの まなビタミン By 東京個別指導学院




比例のグラフの問題 aの値でグラフが右上がりかの判断をしよう 中学や高校の数学の計算問題
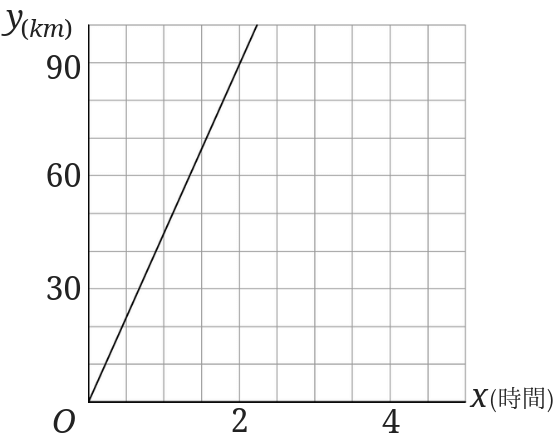



小学生の比例でグラフから式を求める時ってどうするの みけねこ小学校
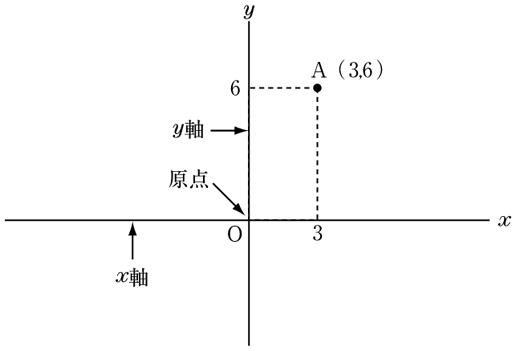



比例のグラフ 算数用語集



比例関係とは 1分でわかる意味 グラフ 正比例との違い 負比例



Studydoctor比例のグラフの利用 動点の問題の解き方 中学1年数学 Studydoctor




中1数学 比例のグラフ1 Y 2xなど 映像授業のtry It トライイット



二乗に比例とは 1分でわかる意味 式 グラフ 例 比例との違い




反比例 式を作る Aを求める 方法はたったコレだけ グラフからの読み取りも簡単 数スタ
コメント
コメントを投稿